GWAS关联分析课程推荐：https://bdtcd.xetslk.com/s/2KgXQq

对于统计学假设检验来说，多重检验校正是一个非常重要的领域。我们在进行假设检验的时候，通常会设置一个零假设，之后计算出一个p值，即数据分布符合原假设的概率，p值越低，即代表拒绝原假设的概率越大。我们通常认为p值＜0.05是一个判断是否显著的阈值。但是在对多组数据同时进行比较的时候，简单地使用0.05作为阈值可能就不那么合适了。换句话说，在同时对多组数据进行处理和比较的时候，很可能其中部分数据因为随机效应而超过阈值，造成假阳性结果。而检验的次数越多，出现假阳性的概率就越大。而对于GWAS等对全基因组的位点进行统计学检验的分析，就急需一种方法来对结果的阈值进行校正。

Bonferroni校正即为最严格的多重检验矫正方法。其校正原理为：在同一数据集上同时检验n个相互独立的假设，那么用于每一假设的统计显著水平，应为仅检验一个假设时的显著水平的1/n。如以显著水平0.05检验同一数据集上两个独立的假设，此时用于检验该两个假设应使用更严格的0.025；对于10000个基因的检验，若将p设置为1e-6，进行10000次比较之后犯错误的概率是10-6*10000 = 0.01，严格地控制了假阳性的出现。

Bonferroni校正的主要应用范围就是GWAS，即全基因组关联分析。在全基因组关联分析中，如果对每个位点进行测试，以0.05的水平进行筛选，由上文可知，在1000000个位点中其假阳性的位点可能达到5%，即50000个，所以，为了控制假阳性的概率，以Bonferroni校正对阈值进行调整。Bonferroni校正会将设定的显著性水平除以测试次数，最终得到一个总的阈值。换句话说，它将阈值从a = 0.05调整为a =（0.05 / n），其中n是进行的统计检验的次数，即SNP的个数。最终得到的阈值根据进入分析的SNP数量不同会有较大的差异，但通常都会在1e-6以下的量级。

当然了，Bonferroni校正作为最严格的的多重假设检验校正方法，在实际应用当中也会出现一些问题。由于GWAS标记之间的连锁不平衡，可能会存在多个标记或者SNP之间相互连锁的情况，也就是说它们之间的分布并不是完全独立的，所以假设GWAS数据集的每个关联测试都是独立的是不正确的。因此，应用Bonferroni校正通常会为我们提供最保守的p值阈值。例如将1000000个位点纳入计算当中，Bonferroni校正所产生的阈值即为5e-8，由于其过为保守，往往会导致假阴性的产生，可能整个基因组中都很少有标记的关联p值能够达到这一标准。这时我们往往需要根据实际曼哈顿图的情况对阈值进行一些调整。

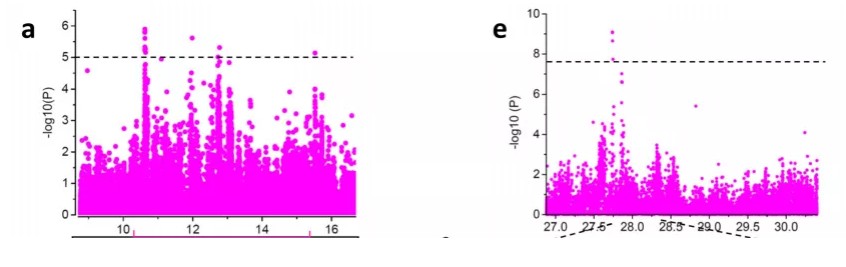
例如2019年Genome Biology桃重测序中的GWAS部分，大多数性状采用的均是经过Bonferroni校正的约3e-8的阈值，但是对于果实大小性状的GWAS分析，研究者将阈值降到了1e-5，以消除由于Bonferroni校正过于严格导致的假阴性。我们可以看到左图中虽然信号强度相对较低，但是有一簇SNP明显呈现连锁的信号，说明可能这里存在着一个与性状关联的QTL。

参考文献：

Li Y, Cao K, Zhu G, et al. Genomic analyses of an extensive collection of wild and cultivated accessions provide new insights into peach breeding history. Genome biology, 2019, 20(1): 36.