z-Transform数据得到z-score方法公式
z-Transform
Sometimes one has the problem to make two samples comparable, i.e. to compare measured values of a sample with respect to their (relative) position in the distribution. An often used aid is the z-transform which converts the values of a sample into z-scores:
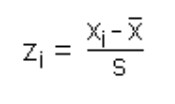
with
zi ... z-transformed sample observations
xi ... original values of the sample... sample mean
s ... standard deviation of the sample
The z-transform is also called standardization or auto-scaling. z-Scores become comparable by measuring the observations in multiples of the standard deviation of that sample. The mean of a z-transformed sample is always zero. If the original distribution is a normal one, the z-transformed data belong to a standard normal distribution (μ=0, s=1).
The following example demonstrates the effect of the standardization of the data. Assume we have two normal distributions, one with mean of 10.0 and a standard deviation of 30.0 (top left), the other with a mean of 200 and a standard deviation of 20.0 (top right). The standardization of both data sets results in comparable distributions since both z-transformed distributions have a mean of 0.0 and a standard deviation of 1.0 (bottom row).
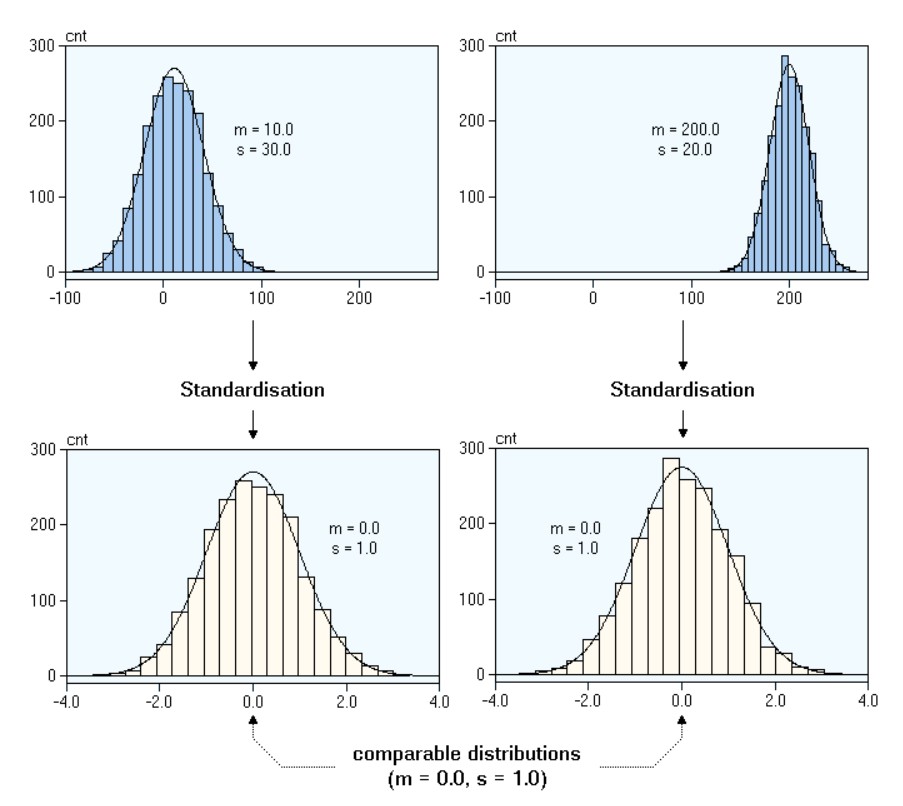
| Hint: | In some published papers you can read that the z-scores are normally distributed. This is wrong - the z-transform does not change the form of the distribution, it only adjusts the mean and the standard deviation. Pictorially speaking, the distribution is simply shifted along the x axis and expanded or compressed to achieve a zero mean and standard deviation of 1.0. |
- 发表于 2020-11-18 17:40
- 阅读 ( 4385 )
- 分类:其他
