cox模型评估-决策曲线分析(DCA)
DCA曲线
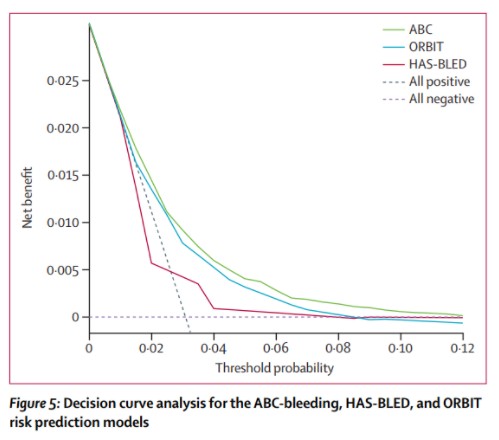
DCA曲线,即决策曲线分析法(Decision Curve Analysis),是用来帮助确定高风险患者进行干预,而低风险患者避免干预(避免过度医疗),即评价患者获益程度的一种评估方法。下图是2016年柳叶刀发表的一篇文章,文中首次进行了DCA曲线的应用。如下图所示,横坐标为阈概率,当各种评价方法达到某个值时,患者i的出血风险概率记为Pi;当Pi达某个阈值(记为Pt),就界定为阳性,采取某种干预措施后,将改变出血与血栓形成之间的利弊平衡,利弊之差即为净获益(Y轴:Net benefit).图中有两条虚线,横着的那条虚线表示所有样本均不进行干预,净获益为0,斜的虚线表示所有样本均进行干预。三条彩色曲线表示三种方案(模型),HAS-BLED曲线与两条虚线有交叉,因此该方案没有价值,而另外两条有价值,相比之下,ABC在ORBIT之上,价值更大。
#加载包rm(list = ls()) library(survival) library(ggDCA) library(rmda) data(lung) lung <- na.omit(lung) lung$status[lung$status==1] <- 0 lung$status[lung$status==2] <- 1 #构建两个模型 fit1 <- coxph(Surv(time,status)~age,data = lung) fit2 <- coxph(Surv(time,status)~age+sex+inst+ph.ecog+ph.karno,data = lung) #绘制单个模型的DCA曲线 plot1 <- dca(fit1,times = 365) ggplot(plot1)
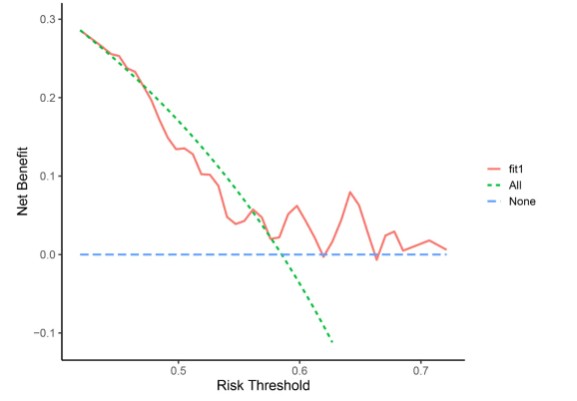
#绘制两个模型的DCA曲线 plot2 <- dca(fit1,fit2,times = 365) ggplot(plot2)
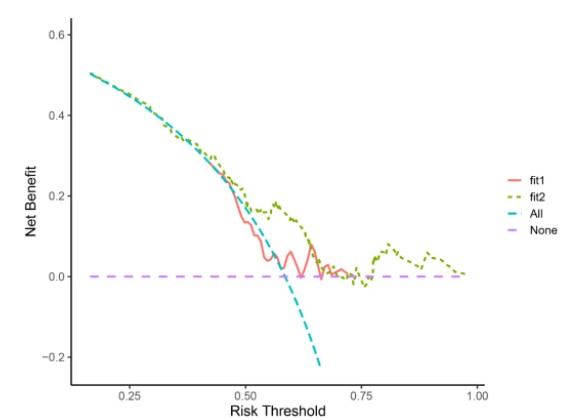
在开始之前,我们先来思考一下:为什么要做DCA决策曲线?5s时间大家可以想一下。
我就接着说啦,首先我们需要明确一点:模型预测的再准确,也不能百分百准确,始终有假阳性和假阴性存在。而我们是根据模型预测结果去判断是否对病人进行干预,这里面就有一个进行干预到底划不划算的问题。
举个例子来说:我们通过某个模型来预测患者是否患病,患病的患者则进行手术切除,不患病的患者则进行药物治疗,无论选取了哪个值为阈值,都会遇到假阳性的可能,假阳性的病人也会接受手术切除,而这个切除可能并不利于患者本身情况甚至患者进行手术切除风险会更大。有时候我们希望避免假阳性,有时候则更希望能避免假阴性。理想的的预测模型在临床使用中,应该在任何时候依照模型预测结果进行干预获得的净受益都比默认的好(最常见的默认情况就是全部干预和全部都不干预)。如果两种情况无法避免,那我就想要找到一个净受益最大的办法。这就是临床效用问题,也是我们为什么做DCA决策曲线的原因。2
下面先和大家介绍4个概念便于理解:
第一:P,意思是给真阳性患者施加干预的受益值(比如通过某模型预测某患者有癌症,实际患者确实患癌,予以活检,达到了确诊的目的);
第二:L,意思是给假阳性患者施加干预的损失值(比如通过某模型预测患者有癌症,而患者实际只是增生,那我们给患者做活检,让ta白白受了一刀);
第四:Pt,阈值,可以理解为模型用来界定是否患病的临界值,大于阈值则为患病,小于阈值的则未不患病;
第四:Pi,患者i患有癌症的概率,当Pi>Pt时为阳性,给予干预。也就是说这个患者的患病概率已经高于我们模型判断是否患病的临界值了,这时候就预测患者患病,并给予干预。
所以较为合理的干预的时机是,当且仅当Pi×P>(1-Pi)×L,即预期的受益高于预期的损失。推导一下可得,Pi>L/(P+L)即为合理的干预时机,于是把L/(P+L)定义为判断患者是否患病的阈值Pt。
净收益(NB)指的是干预的净收益,可以理解为 真实患病的人的比例(也就是真阳性的比例,用A表示)*给真阳性患者施加干预的受益值(P)-真实不患病但模型预测患病的人的比例B(也就是假阳性的比例,用B表示),公式可以表示为:NB=A×P–B×L;注意:这里的比例都是用全部样本去算的。
以阈值Pt为横坐标,净收益NB为纵坐标,画出来的曲线就是DCA决策曲线。
讲完基本概念我们来看实际案例
这张DCA曲线图它横坐标为风险阈值Pt,纵坐标为利减去弊之后的净获益NB。当各种评价指标达到某个值时,患者i的死亡风险概率记为Pi;当Pi达某个阈值(Pt)时,就界定其为阳性,采取某种干预措施。纵坐标就是利减去弊之后的净获益率也就是前文提到的NB。
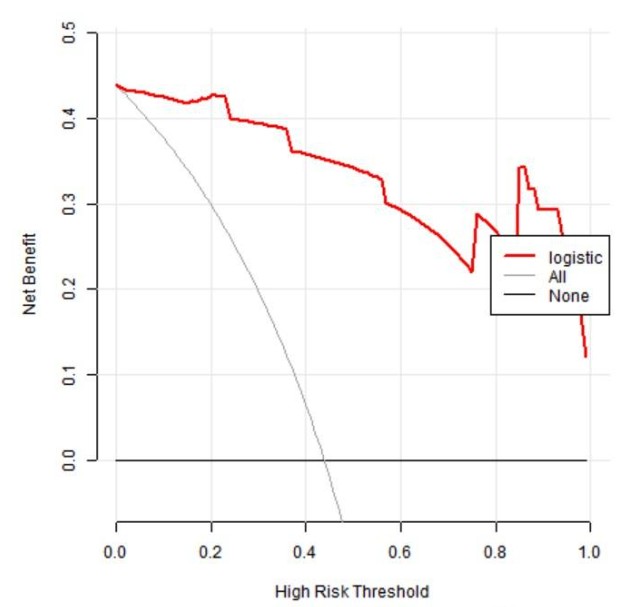
图中的红色线表示在每个风险阈值下的净收益,其他两条线,代表两种极端情况。横的那条黑色直线表示,所有样本都是阴性(Pi < Pt),所有人都不施加干预的情况,都不干预了哪来的干预净收益,所以此时不论阈值为多少干预的净获益都是0,因此是一条横线。斜的那条灰色线表示所有样本都是阳性,所有人都接受了干预,在不同阈值下该批样本在该模型下的净收益。举个图中具体的点来看,假设我们设定阈值为0.6,患者的阈值如果高于0.6,我们就认为其需要进行干预治疗,我们可以看到它的净收益差不多在0.3左右,如果我们的样本量为1000人,那这个意思就是施加干预后能受益的人为300人。
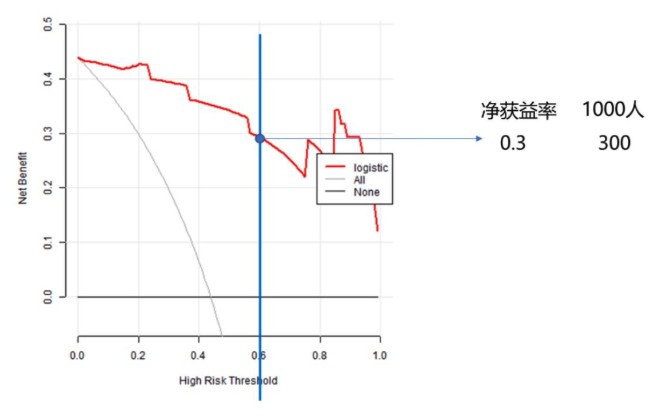
DCA决策曲线是评价预测模型临床效用的方法,从图中可以看出,在一个很大的阈值Pt区间内,模型的获益都比极端曲线高,所以它们可选的阈值Pt范围都比较大,相对而言比较安全,可以结合实际的净收益情况去选择阈值的大小。
本期干货内容有点多,对大家如果有一点点帮助,还请大家多多支持,关注我呀~
今天就到这啦,感谢大家支持!我们下期再见,拜拜~
参考文献:
1. Vickers AJ, Elkin EB. Decision curve analysis: a novel method forevaluating prediction models. Med Decis Making.2006;26(6):565-574.
2. Vickers AJ, van Calster B, Steyerberg EW. A simple, step-by-step guide to interpreting decision curve analysis. Diagn Progn Res.2019;3:18. Published 2019 Oct 4.
3. Van Calster B, Wynants L, Verbeek JFM, et al. Reporting and Interpreting Decision Curve Analysis: A Guide for Investigators.Eur Urol. 2018;74(6):796-804.
4. Yan P, Li JW, Mo LG, Huang QR. A nomogram combining inflammatory markers and clinical factors predicts survival in patients with diffuse glioma. Medicine (Baltimore). 2021;100(47):e27972. doi:10.1097/MD.0000000000027972
参考:https://zhuanlan.zhihu.com/p/671116874
- 发表于 2021-08-16 16:28
- 阅读 ( 17957 )
- 分类:TCGA
你可能感兴趣的文章
- univariate_cox.r 临床数据单因素cox回归分析 6184 浏览
- multi_cox.r 基因表达量做多因素cox分析 5759 浏览
- lasso_cox.r lasso_cox 模型优化分析 8747 浏览
- univariate_cox_batch.r 基因表达量批量单因素cox回归分析 5924 浏览
- R语言-Cox比例风险模型 5345 浏览
